수학 - 벡터의 연산

벡터의 덧셈, 뺄셈, 분해

일단 제일 간단한 덧셈을 해보자 덧셈을 하려면 일단 분해에 대한 이해가 있어야 된다.

위의 A벡터는 B, C라는 벡터로 분해가 된다. 결국에 B + C의 합이 A가 됬기 때문에 

벡터 A는 B + C의 합으로 표현 될 수 가 있다. 

이제 두 벡터를 한번 더해보자

두 벡터를 일단 분해를 한뒤에 각각의 축성분끼리 따로 더해준다.

다시 축에따라서 덧셈을 해주면 된다.

덧셈은 A + B = B + A의 교환법칙도 성립한다.

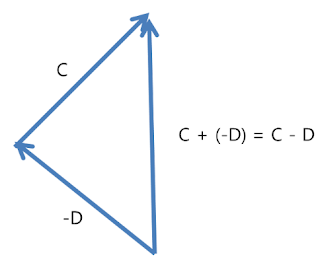
뺄셈의 경우에는 

위와 같이 벡터를 반전시켜서 더하는 것과 같다.

벡터의 내적

내적은 스칼라곱이라고도 하며 기호로 a · b (Dot)점을 쓴다.

두 벡터 사이의 각도를 구한다고 이해하면 될 것같다.

방법은 두가지가 있는데 첫번째로 

좌표값의 각 성분들을 곱해서 더하는 방법이있다.

두번째는

벡터D의 크기는 벡터A의 크기에 cosθ를 곱한것이다. 

프로그래밍에서는 보통 A, B벡터의 단위벡터로 계산을 한다.

단위 벡터로 계산을 해보면 결국에 cosθ값이 나오게 된다.

이런식으로 cosθ값으로 방향과 뻗어있는 비율?을 알수가 있다.

A · B = 0 이면 , A와 B의 벡터는 직교 ㅗA · B < 0 이면 , 90 < Θ < 180 -90 < Θ < -180
A · B > 0 이면 , 0 < Θ < 90도 , -90 < Θ < 0

스칼라 값이기 때문에 역시 A · B = B · A 성립한다.

벡터의 외적

외적은 다른연산들 과는 다르게 3차원공간에서만 사용이 가능하다.

외냐하면 외적을 하면 두벡터의 수직벡터로 벡터가 하나 더생기는 특이한 연산이기때문이다.

방향은 두 벡터에 대해서 수직이고 크기는 두벡터의 평행사변형의 넓이와 같다.

계산법은 위와 같다.

벡터가 새로생기는 연산이기때문에 교환법칙이 성립할 수 없다.

외적또한 단위벡터를 써서 계산하게 되면 C의 크기를 통해

A, B의 사이각을 구하고 방향을 판단 할 수 있다.